Harri Roblin

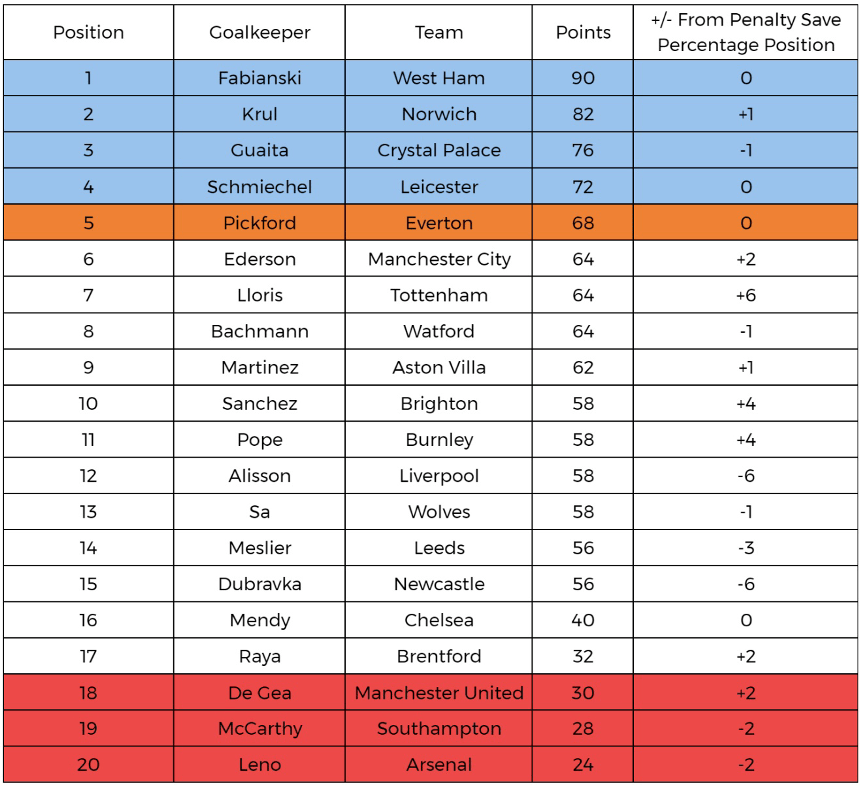
An algorithm was created using Python to predict a penalty shootout between all of the Premier League’s sides. The goalkeeper’s career penalty save percentage was obtained from the FBRef database. A random number generator from 0 to 100 was used and if the number was below the save percentage, the penalty was saved. Loops were used to repeat this code 5 times for each team and the penalty score was then recorded. If the scores are equal after the 5 repetitions, sudden death will start in the form of additional loops. The algorithm was then used to simulate a Premier League season of penalty shootouts (38 games per side) and the results are printed below.

Fabianski won the most penalty shootouts racking up 90 points, which is driven by his penalty save percentage being the highest in the league. The three relegated sides are Manchester United, Southampton and Arsenal. This is interesting as Bernd Leno and David De Gea are two of the best open-play shot-stoppers in the league. This means their problem is reading penalty-takers, not the actual saving if they go the right direction. All the newly promoted sides stay up in this format, with Krul and Norwich finishing second in the league. Krul is acknowledged as one of the best penalty savers in the league. He is well known for being subbed on for the penalty shootout against Costa Rica in the 2014 World Cup, saving 2 penalties and winning the game for the Netherlands.

On the far right of the table, it shows who under and over performed the most in this algorithm based on a simple ranking of percentage of penalties stopped in their career. Dubravka and Alisson are both the biggest under performers, dropping 6 places further down the table than they should be. Lloris is the main benefactor of these dropped places, rising 6 places higher than predicted. I think the variety in these positions adds to the validity of the algorithm, as it simulates the unpredictability of penalty shootouts. The best career penalty stopping goalkeeper does not always win in a penalty shootout and the algorithm supports this.

There are two ways this algorithm can be improved. Firstly, in regular game-time, the goalkeeper’s career penalty save percentage will largely be against a team’s best penalty taker. This means it is a worst case scenario for a goalkeeper and in reality, they would probably save more penalties as the penalty shootout progresses and the less experienced takers step up. Also, this algorithm could be improved by quantifying the quality of a team’s set of penalty takers, however, I could not obtain these stats due to a lack of data sources. The random generator is therefore a reasonable way to simulate each penalty taker and a random quality of shot.